- Get link
- X
- Other Apps
Buktikan bahwa 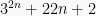 habis dibagi 5.
habis dibagi 5.
Pembahasan :
- Langkah 1
- Langkah 2 (n = k)
- Langkah 3 (n = k + 1)
dengan bentuk soal)
Didapatkan :
habis dibagi 5
habis dibagi 5
sama dengan langkah 2, habis dibagi 5
- Get link
- X
- Other Apps
