Buktikan bahwa \frac{1}{2} + \frac{2}{2^2} + \frac{3}{2^3} + \cdots + \frac{n}{2^n} = 2 - \frac{n + 2}{2^n}
- Get link
- X
- Other Apps
Buktikan bahwa 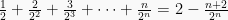
Pembahasan :
- Langkah 1
- Langkah 2 (n = k)
- Langkah 3 (n = k + 1)
Dibuktikan dengan:
- Get link
- X
- Other Apps
